切披萨的方案数题解

Posted on Edited on

切披萨方案数题解

原题

Leetcode 切披萨方案数

查看原题

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： ‘A’ （表示苹果）和 ‘.’ （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含 至少 一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

1
2
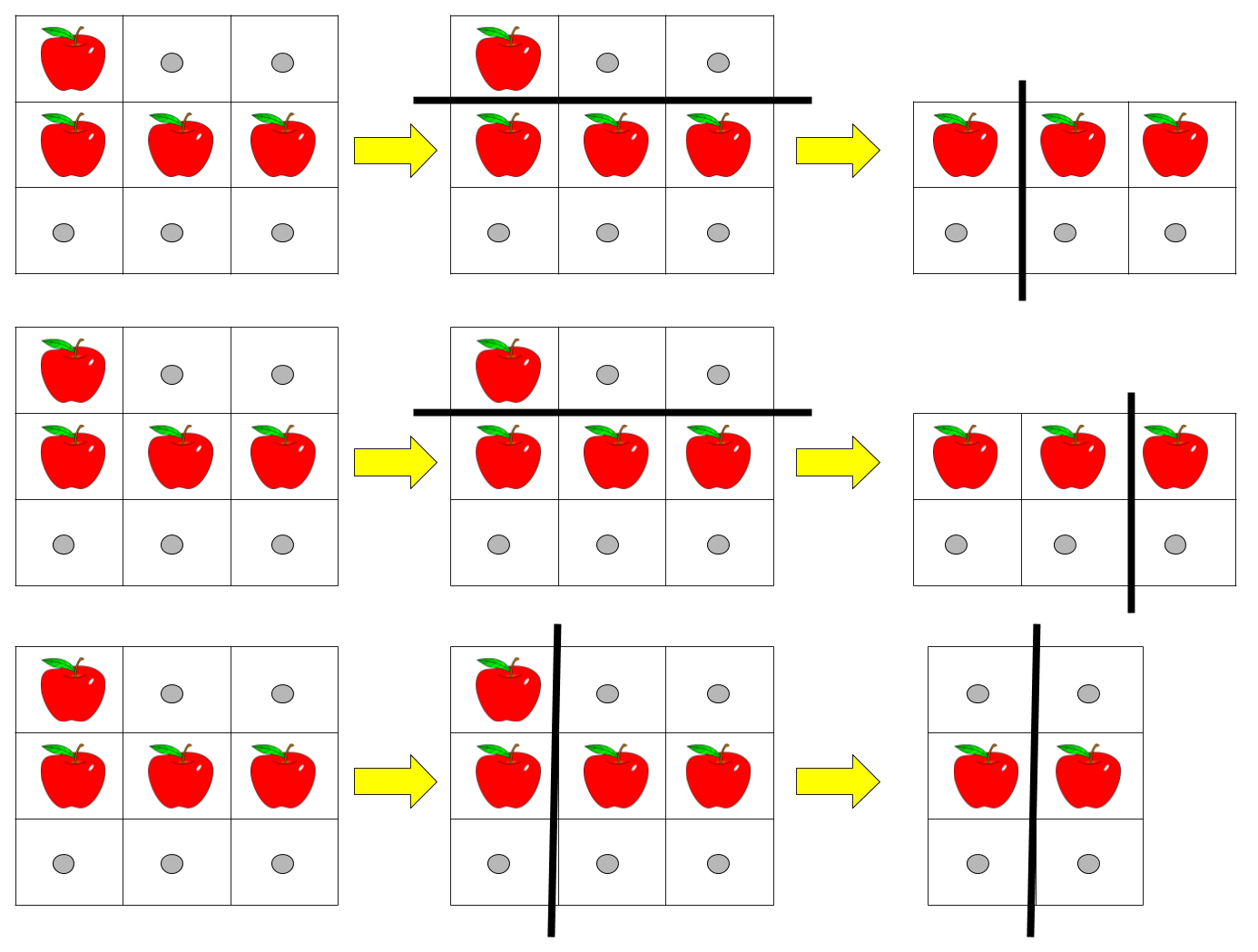
3
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

1
2
输入：pizza = ["A..","AA.","..."], k = 3
输出：1

示例 3：

1
2
输入：pizza = ["A..","A..","..."], k = 1
输出：1

提示：

1
2
3
4
5
1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

分析

前置说明

为了描述方便，我们用 披萨（i, j） 表示左上角坐标为 (i, j) 右下角坐标为(rows -1 ,cols-1) 的披萨

使用 dp 变量表示状态

dp[i][j][k] 表示 披萨（i, j） 切 k 次 分给 k+1个人 一共有多少种情况

拿例一中的图举例：

dp[2][2][0] == 0 表示下图的红框中的披萨切0次，分给1个人，共有 0 种情况。

dp[1][1][1] == 1 表示下图红框中的披萨切1次，分给 2个人，共有1情况

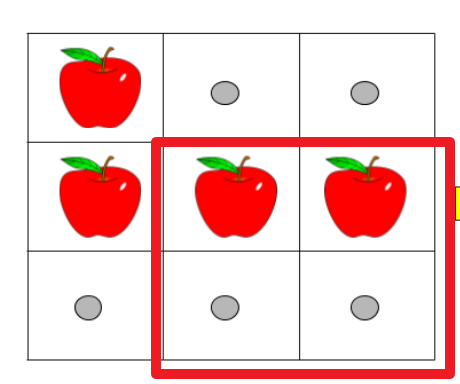
题目中所求的即为 dp[0][0][k-1] 的值，他代表的意思为，从 披萨（0, 0）中切 k-1 次分给 k 个人的情况数

状态转移方程

dp 算法的关键是，如何将一个问题转化为子问题进行求解，即写出状态转移方程。

公式

$$dp[i][j][k] = \sum_{r=i+1}^{rows-1}(hasApple(i,j,r,j) ? dp[r][j][k-1] : 0) + \sum_{r=j+1}^{cols -1}(hasApple(i,j,i,r) ? dp[i][r][k-1] : 0)$$

其中：

$$hasApple(i,j,i,j) = remains[i]][j] - reamains[i][j] > 0$$

解释

dp[i][j][k]

对于任意的 披萨 (i, j)，我们遍历他们所有的切割方法（包括横切和纵切），记每种切割完后剩余的披萨为 (i', j')，则剩下的披萨的切割情况数可以用dp[i'][j'][k-1]来表示，我们将所有的这些满足条件的子情况数加起来，就得到了dp[i][j][k]

hasApple

代表切下来的部分是否含有苹果。

remains[i][j] 数组表示披萨 (i, j) 包含的苹果总数

记切除后的披萨为 披萨（i', j'）

则切下来的部分的披萨包含苹果数就可以用 remains[i][j] - remains[i'][j'] 来表示了

如何求 remains 数组

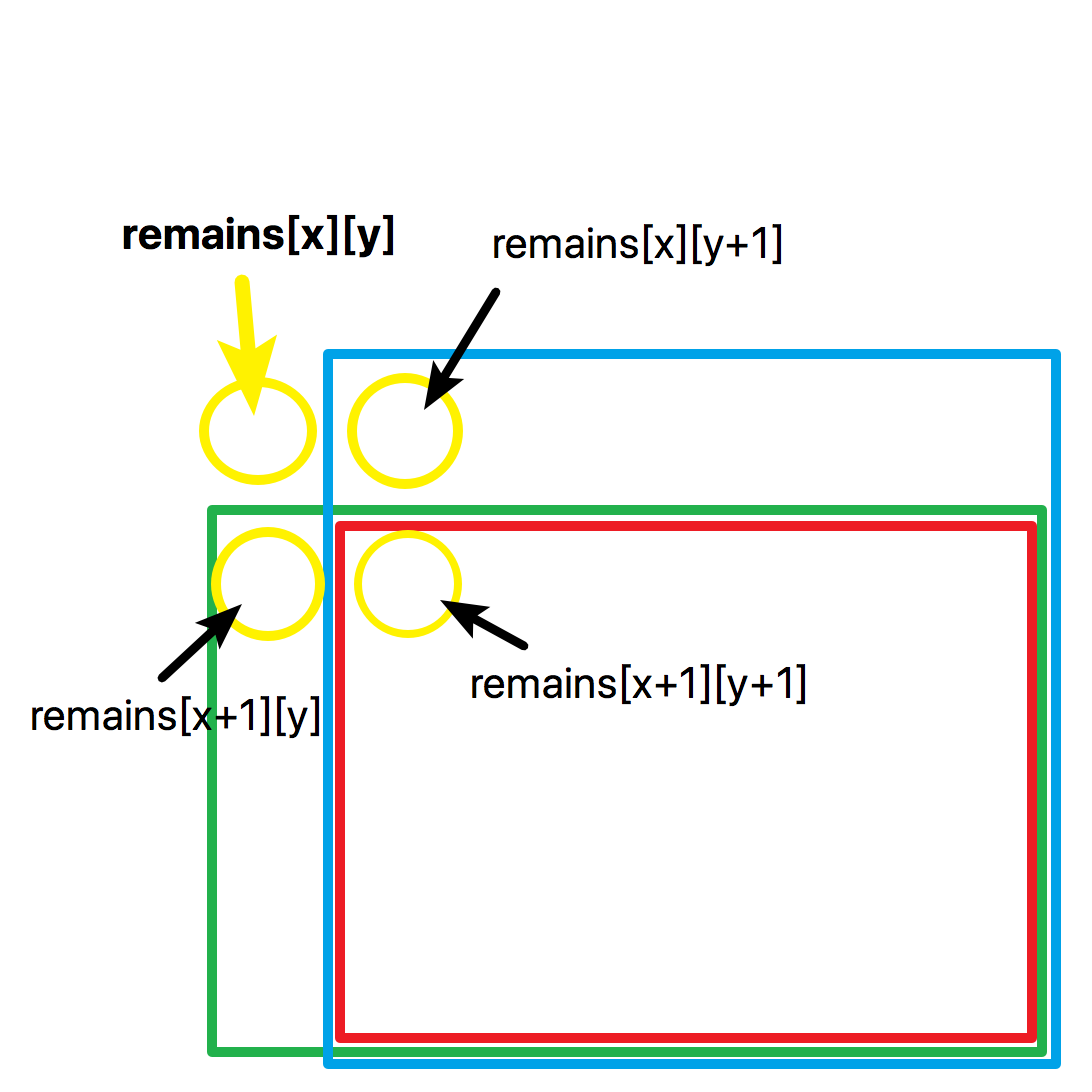
我们观察上图，remains[x][y] 的值就等于 他本身 + 绿色的框 + 蓝色的框 - 红色的框（重复叠加了）

即 $remains[x][y] = current + remains[x+1][y] + remains[x][y+1] - remains[x+1][y+1] $

通过上述dp转移方程，我们算出披萨中的每个点的remains值存在数组中备用。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
var ways = function (pizza, k) {
  let row = pizza.length;
  let column = pizza[0].length;
  let remains = new Array(row).fill(null).map((each) => []);
  let mod = 1e9 + 7;

  for (let i = row - 1; i >= 0; i--) {
    for (let j = column - 1; j >= 0; j--) {
      let current = pizza[i][j] === 'A' ? 1 : 0;
      if (i === row - 1) {
        remains[i][j] = (remains[i][j + 1] || 0) + current;
        continue;
      }
      if (j === column - 1) {
        remains[i][j] = (remains[i + 1][j] || 0) + current;
        continue;
      }

      remains[i][j] =
        remains[i][j + 1] + remains[i + 1][j] + current - remains[i + 1][j + 1];
    }
  }

  let dp = [];
  for (let i = 0; i < row; i++) {
    dp[i] = new Array();
    for (let j = 0; j < column; j++) {
      dp[i][j] = new Array(k).fill(0);
    }
  }

  for (let i = row - 1; i >= 0; i--) {
    for (let j = column - 1; j >= 0; j--) {
      if (remains[i][j] > 0) dp[i][j][0] = 1;

      for (let cut = 1; cut < k; cut++) {
        // 横着切
        for (let r = i + 1; r < row; r++) {
          if (remains[i][j] - remains[r][j] > 0) {
            dp[i][j][cut] = (dp[r][j][cut - 1] + dp[i][j][cut]) % mod;
          }
        }
        // 竖着切
        for (let r = j + 1; r < column; r++) {
          if (remains[i][j] - remains[i][r] > 0) {
            dp[i][j][cut] = (dp[i][r][cut - 1] + dp[i][j][cut]) % mod;
          }
        }
      }
    }
  }
  return dp[0][0][k - 1];
};